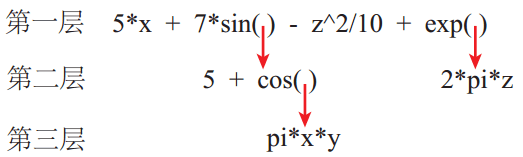文本函数解析树算法

Ruichen Ni

需求来源

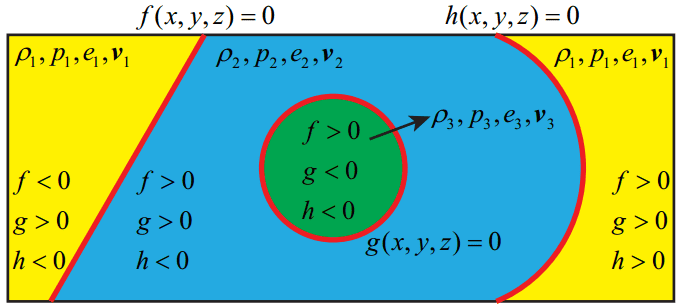
多介质流场的初始状态可能存在物质界面和激波等多种间断面，在初始化过程中间断面两侧需要赋予不同的流场参数，如图1所示。一种较为简单且通用的做法是直接通过输入文件读入每一个计算域网格格心的流场初始状态。然而当计算域网格发生变化（例如网格加密）或流场初始状态需要微调时都需要重新生成输入文件，另外针对大型算例撰写相应的初始状态输入文件也费时费力且容易出错。一般而言，初始状态下的间断面通常较为规则，可以通过如图1所示的解析函数进行描述。

Flow Initial State
图1：流场初始状态

为了能够统一地处理从输入文件中读入的各类解析函数，并且避免GB级甚至TB级的数据文件读取，本文实现了文本函数解析树算法，能够处理各类双目运算符和单目函数。将读入的解析函数 \(f(x,y,z)\)作为判别式函数，可以划分计算域为正区域 \(\Omega_{f+} \)和负区域 \(\Omega_{f-}\)

$$ \begin{equation} f(x,y,z) = \left\{ \begin{aligned} &> 0,\quad (x,y,z)\in\Omega_{f+} \\ &<0,\quad (x,y,z)\in\Omega_{f-} \end{aligned} \right. \end{equation} $$

因此将间断面的函数表达式作为判别式函数对流场区域进行分区，就可以统一且高效地对任意流动问题进行初始化。例如图1中的流场初始状态可以通过下式给出

$$ \begin{equation} (\rho,p,e,\bf{v})=\left\{ \begin{aligned} &(\rho_1,p_1,e_1,\bf{v}_1),\quad \bf{x}\in \Omega \setminus \left\{ \Omega_{f +} \cap \Omega_{h -} \right\} \\ &(\rho_2,p_2,e_2,\bf{v}_2),\quad \bf{x}\in \Omega_{f +} \cap \Omega_{h -} \cap \Omega_{g +} \\ &(\rho_3,p_3,e_3,\bf{v}_3),\quad \bf{x}\in \Omega_{g -} \end{aligned} \right. \end{equation} $$

文本函数解析需求

  1. 函数自变量只能是空间坐标\((x, y, z)\)，不区分大小写。
  2. 函数支持的双目运算符为加法“\(+\)”、减法“\(-\)”、乘法“\( \ast \)”、除法“\(/\)”和乘方“\(\land\)”，并且所有运算符均不能省略，例如\(x\ast y\)不能简写为\(xy\)。
  3. 函数支持的单目函数有：三角函数\(\sin()/\arcsin()/\cos()/\arccos()/\tan()/\arctan()\)、对数函数\(\log()/\log10()\)、指数函数\(\exp()\)、平方根函数\(\text{sqrt}()\)、绝对值函数\(\text{abs}()\)以及空函数\(()\)。其中将括号当作空函数处理可以简化算法流程，并且所有函数的左右括号必须合法配对。
  4. 函数支持的常量系数为圆周率\(\text{pi}\)和自然常数\(e\)，并且均保留15位有效数字参与运算。

文本函数解析流程

我们将通过如下的示例文本函数来说明文本函数解析树算法的流程。

5*x + 7*sin(5 + cos(pi*x*y)) - z^2/10 + exp(2*pi*z)

首先根据左右括号的配对情况划分函数层次，每对括号内部的函数表达式层次加1。示例函数的层次情况如图2所示。

Formula Architecture
图2：示例函数分层

其次针对每层中的每一个函数表达式划分基本运算符和数据，并赋予计算优先级。以图2中的第一层为例

  1. 函数表达式对应的上一层函数为：空函数\(()\)
  2. 基本运算符按顺序依次为：\(\ast\)、\(+\)、\(\ast\)、\(-\)、\(\land\)、\(/\)和\(+\)
  3. 数据按顺序依次为：5、\(x\)、7、\(\sin()\)、\(z\)、2、10和\(\exp()\) 其中数据的计算优先级为0，加法和减法的计算优先级为1，乘法和除法的计算优先级为2，以及乘方的计算优先级为3。

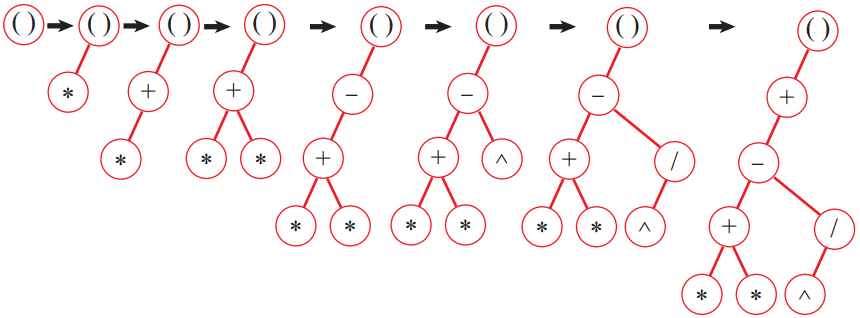
然后，以上一层函数作为根节点将上述基本运算符序列根据计算优先级生成基本运算符树：比较待插入运算符与当前节点运算符的计算优先级，如果待插入运算符的优先级较高就探寻当前节点的右子节点；否则替代当前节点，并将当前节点置为自己的左子节点。目前仅处理双目运算符和单目函数，因此根节点只有左子节点，而所有基本运算符节点都有两个子节点。示例函数第一层函数表达式的基本运算符树构建过程如图3所示。

first-layer-operator
图3：示例函数第一层函数表达式的基本运算符树构建过程

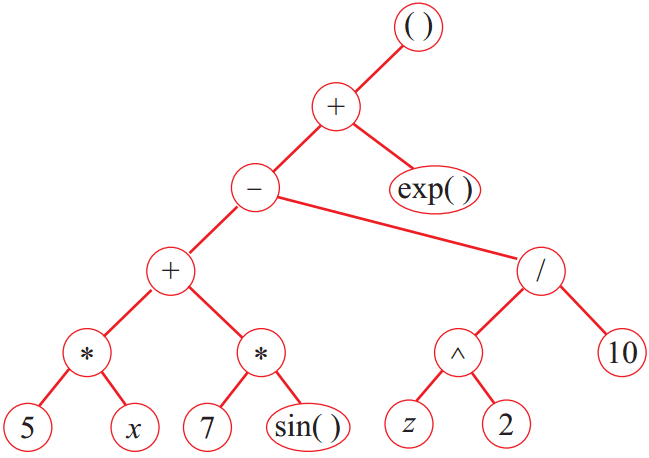
最后将数据序列通过后序遍历依次添加到基本运算符树的叶子节点处，就可以得到每一层每个函数表达式的解析树。示例函数第一层函数表达式的解析树如图4所示。然后根据对应关系将每个解析树中的函数数据节点替换为下一层中以此函数为根节点的解析树，即可得到整个文本函数的解析树。

first-layer-whole
图4：示例函数第一层函数表达式的解析树

对上述文本函数解析树进行后序遍历并将相应的自变量替换为待计算的空间点坐标\(\bf{X}_0=(x_0,y_0,z_0)\)，即可得到空间点\(\bf{X}_0\)处的函数值。